경주로 건설

문제 설명

건설회사의 설계사인 죠르디는 고객사로부터 자동차 경주로 건설에 필요한 견적을 의뢰받았습니다.
제공된 경주로 설계 도면에 따르면 경주로 부지는 N x N 크기의 정사각형 격자 형태이며 각 격자는 1 x 1 크기입니다.
설계 도면에는 각 격자의 칸은 0 또는 1 로 채워져 있으며, 0은 칸이 비어 있음을 1은 해당 칸이 벽으로 채워져 있음을 나타냅니다.
경주로의 출발점은 (0, 0) 칸(좌측 상단)이며, 도착점은 (N-1, N-1) 칸(우측 하단)입니다. 죠르디는 출발점인 (0, 0) 칸에서 출발한 자동차가 도착점인 (N-1, N-1) 칸까지 무사히 도달할 수 있게 중간에 끊기지 않도록 경주로를 건설해야 합니다.
경주로는 상, 하, 좌, 우로 인접한 두 빈 칸을 연결하여 건설할 수 있으며, 벽이 있는 칸에는 경주로를 건설할 수 없습니다.
이때, 인접한 두 빈 칸을 상하 또는 좌우로 연결한 경주로를 직선 도로 라고 합니다.
또한 두 직선 도로가 서로 직각으로 만나는 지점을 코너 라고 부릅니다.
건설 비용을 계산해 보니 직선 도로 하나를 만들 때는 100원이 소요되며, 코너를 하나 만들 때는 500원이 추가로 듭니다.
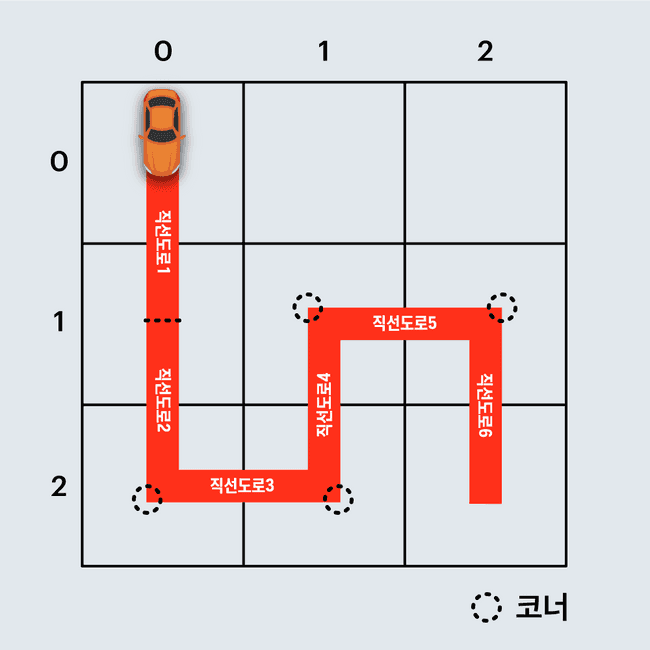
죠르디는 견적서 작성을 위해 경주로를 건설하는 데 필요한 최소 비용을 계산해야 합니다.

예를 들어, 아래 그림은 직선 도로 6개와 코너 4개로 구성된 임의의 경주로 예시이며, 건설 비용은 6 x 100 + 4 x 500 = 2600원 입니다.

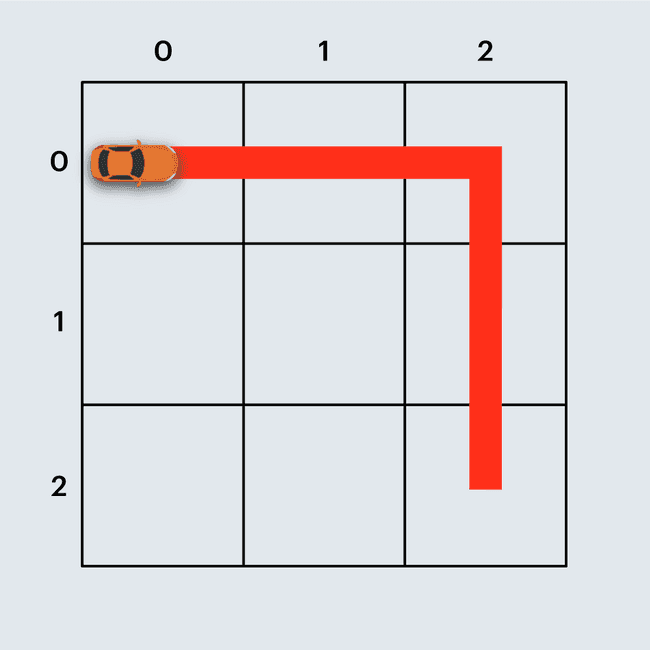
또 다른 예로, 아래 그림은 직선 도로 4개와 코너 1개로 구성된 경주로이며, 건설 비용은 4 x 100 + 1 x 500 = 900원 입니다.

도면의 상태(0은 비어 있음, 1은 벽)을 나타내는 2차원 배열 board가 매개변수로 주어질 때, 경주로를 건설하는데 필요한 최소 비용을 return 하도록 solution 함수를 완성해주세요.

[제한사항]

• board는 2차원 정사각 배열로 배열의 크기는 3 이상 25 이하입니다.
• board 배열의 각 원소의 값은 0 또는 1 입니다.
  • 도면의 가장 왼쪽 상단 좌표는 (0, 0)이며, 가장 우측 하단 좌표는 (N-1, N-1) 입니다.
  • 원소의 값 0은 칸이 비어 있어 도로 연결이 가능함을 1은 칸이 벽으로 채워져 있어 도로 연결이 불가능함을 나타냅니다.
• board는 항상 출발점에서 도착점까지 경주로를 건설할 수 있는 형태로 주어집니다.
• 출발점과 도착점 칸의 원소의 값은 항상 0으로 주어집니다.

입출력 예

board	result
[[0,0,0],[0,0,0],[0,0,0]]	900
[[0,0,0,0,0,0,0,1],[0,0,0,0,0,0,0,0],[0,0,0,0,0,1,0,0],[0,0,0,0,1,0,0,0],[0,0,0,1,0,0,0,1],[0,0,1,0,0,0,1,0],[0,1,0,0,0,1,0,0],[1,0,0,0,0,0,0,0]]	3800
[[0,0,1,0],[0,0,0,0],[0,1,0,1],[1,0,0,0]]	2100
[[0,0,0,0,0,0],[0,1,1,1,1,0],[0,0,1,0,0,0],[1,0,0,1,0,1],[0,1,0,0,0,1],[0,0,0,0,0,0]]	3200

입출력 예에 대한 설명

입출력 예 #1

본문의 예시와 같습니다.

입출력 예 #2

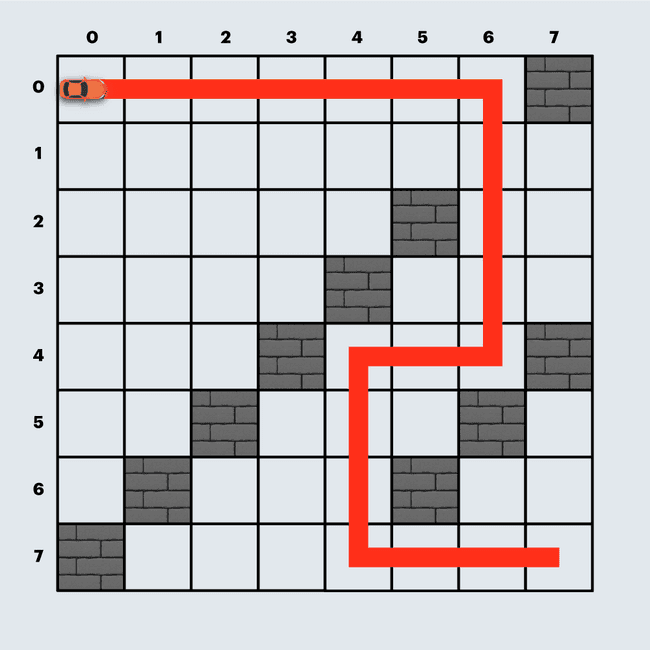
위와 같이 경주로를 건설하면 직선 도로 18개, 코너 4개로 총 3800원이 듭니다.

입출력 예 #3

위와 같이 경주로를 건설하면 직선 도로 6개, 코너 3개로 총 2100원이 듭니다.

입출력 예 #4

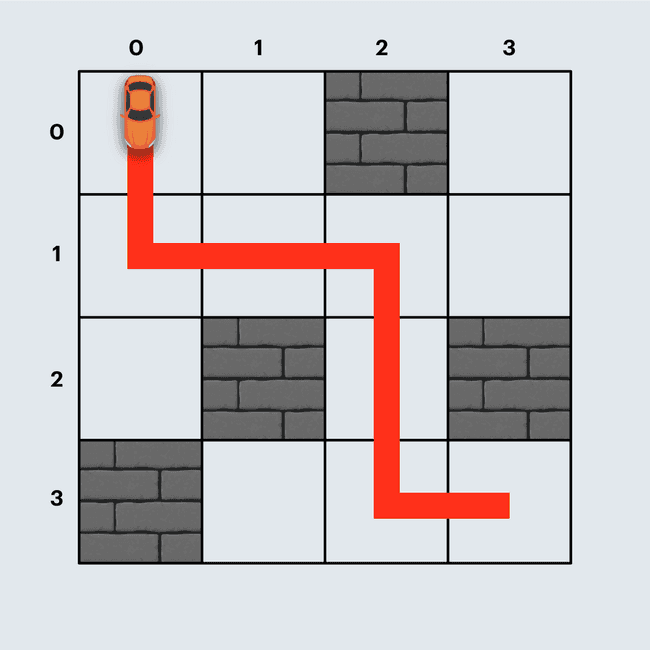
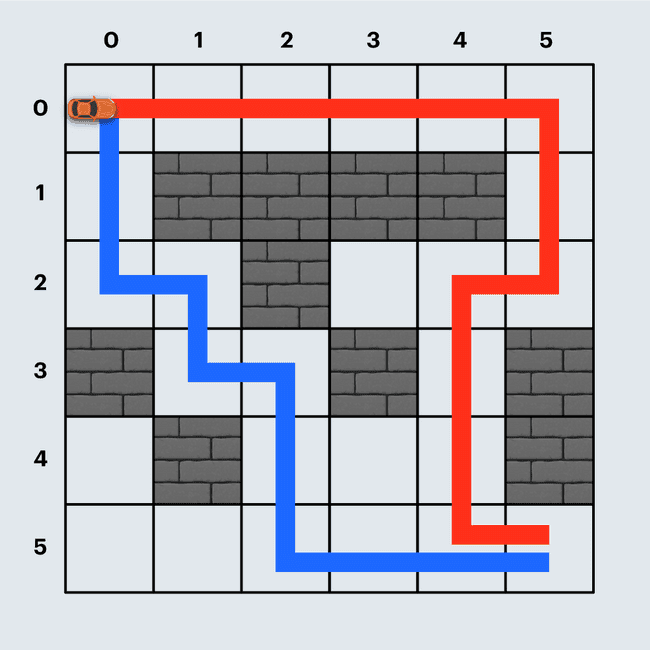
붉은색 경로와 같이 경주로를 건설하면 직선 도로 12개, 코너 4개로 총 3200원이 듭니다. 만약, 파란색 경로와 같이 경주로를 건설한다면 직선 도로 10개, 코너 5개로 총 3500원이 들며, 더 많은 비용이 듭니다.

문제풀이

다익스트라 알고리즘과 최단거리를 합치면 된다.

1. arr배열을 만들어주는데, 해당 좌표의 코스트를 표현해주는 배열인데, 상하좌우 즉 방향을 표현하기 위해서 3차원 0,1,2,3(상하좌우)로 만들어준다.
2. 그리고 arr[0][0] 0,0 좌표에 대해서 상하좌우 모두 0으로 만들어주고 시작한다.
3. queue에다 0,0 좌표를 넣어주고 (0,1,2,3) for문을 시작한다.
4. queue에서 코스트가 잡은 값을 빼고 x,y,direction,cost를 변수로 선언해준다.
5. 상하좌우를 표현하기 위해서 dx,dy배열을 전역변수로 선언해준다.
6. 0,1,2,3(상하좌우)를 돌아야하니까 4만큼 for문을 돌려준다.
7. x,y좌표에 dx[i],dy[i]를 더한 값을 nx,ny로 선언한다.
   1. dir-i가 2일때 -> 왔던길로 되돌아가는 경우 continue;
   2. nx,ny가 정상적인 좌표가 아닐때 && board[x][y]가 1인경우(벽에 막혔을때) continue
8. 위의 경우가 아니라면 , 방향에 따라서 더할 값 즉 cost2를 정해준다(100 or 600)
9. arr[x][y][i] 가 next = cost+cost2보다 작으면 arr[x][y][i]를 next로 바꿔주고, queue에 푸시해준다.
10. board배열에서 board.length-1,board.length-1 중에서 제일 작은 값을 리턴한다.

const dx = [-1, 0, 1, 0];
const dy = [0, -1, 0, 1];
function Point(x, y, direction, cost) {
  let obj = { x, y, dir: direction, cost };
  return obj;
}

function solution(board) {
  var answer = 0;
  const len = board.length;
  let queue = [];
  let arr = [];

  for (let i = 0; i < len; i++) {
    let temp2 = [];
    for (let j = 0; j < len; j++) {
      let temp = [];
      for (let k = 0; k < 4; k++) {
        temp.push(Infinity);
      }
      temp2.push(temp);
    }
    arr.push(temp2);
  }

  for (let i = 0; i < 4; i++) arr[0][0][i] = 0;

  queue.push(Point(0, 0, 0, 0));
  queue.push(Point(0, 0, 1, 0));
  queue.push(Point(0, 0, 2, 0));
  queue.push(Point(0, 0, 3, 0));

  while (queue.length) {
    let point = queue.shift();
    let { x, y, dir, cost } = point;

    for (let i = 0; i < 4; i++) {
      let nx = x + dx[i];
      let ny = y + dy[i];
      if (Math.abs(dir - i) === 2) continue;
      if (nx < 0 || ny < 0 || nx >= len || ny >= len || board[nx][ny] === 1)
        continue;
      let cost2 = dir === i ? 100 : 600;
      let next = cost + cost2;
      if (arr[nx][ny][i] > next) {
        arr[nx][ny][i] = next;
        queue.push(Point(nx, ny, i, arr[nx][ny][i]));
        queue.sort((a, b) => a.cost - b.cost);
      }
    }
  }
  arr[len - 1][len - 1].sort((a, b) => a - b);
  return arr[len - 1][len - 1][0];
}